La Dérivation 1BAC

Fiche de cours

L’objectif ultime de cette année en analyse consiste à tracer toutes fonctions. A ce stade, nous avons appris les connaissances nécessaires pour y arriver. En effet, nous avons commencé par la notion de la fonction pour clarifier ses caractéristiques : domaine de définition, la parité, la monotonie…, puis les limites pour définir les notions de voisinage et de convergence.

Alors, nous traiterons dans ce cours une nouvelle notion en analyse qui est la dérivation, un concept totalement local, autrement nous vérifions la dérivabilité de la fonction en chaque point de son $ D_{f} $. En plus, la dérivation est liée aux variations de la fonction, et elle permet de déterminer son comportement et évidemment elle permet d’aboutir à des interprétations géométriques extrêmement importantes servant à anticiper le trajet de la fonction.

Ensuite, il faut savoir que nous avons déjà confronté cette notion mais sans la nommée, précisément le calcul du coefficient directeur d’une fonction affine, c'est un nombre qui caractérise la « pente » de la droite.

Graphiquement,

Coefficient directeur $ =\frac{\text { Varations des ordonnés }}{\text { varaitions des abcisses }}=\frac{\Delta_{y}}{\Delta_{x}} $

Nous appellerons ce coefficient : le nombre dérivé, qui est unique et constant même si on change les coordonnés car la fonction est affine.

Notion de dérivabilité

Dérivabilité au point

تعريف

Soit $f$ une fonction numérique de domaine définition $D_{f}$, soit $I \subset D_{f}$ un intervalle ouvert tel que $a$ appartient à l'intérieur de $I$. On dit que la fonction $f$ est dérivable en $a$ s'il existe un nombre réel $l$ tel que :

$\lim\limits _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=l \in \mathbb{R}$

Dans ce cas, on appelle $l$ le nombre dérivé de $f$ en $a$, et on le note $f^{\prime}(a)$.

Remarque

On peut reformuler la définition précédente par un changement de variable. On pose $x=a+h$, alors $x \rightarrow a$ quand $h \rightarrow 0$

Donc, la fonction $f$ est dérivable en $a$ si et seulement si $\\[0.2cm]$ $\lim\limits _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}=l=f^{\prime}(a) \in \mathbb{R}$

Interprétation géométrique

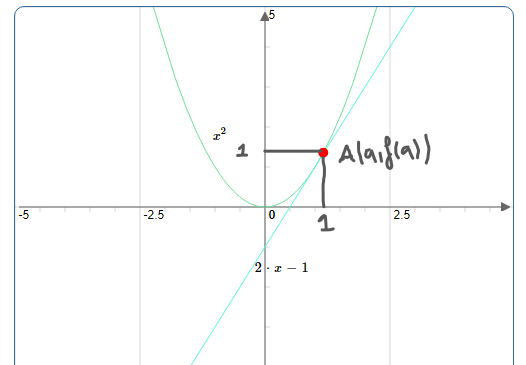
Soit $f$ une fonction dérivable en $a$. Alors le nombre $f^{\prime}(a)$ est la pente de la droite tangente à $\left(C_{f}\right)$, la représentation graphique de $f$, au point $A(a, f(a)) $.

مثال

La fonction $~ f(x)=x^{2}~$ est dérivable en$1$ . En effet,

$\lim\limits _{x \rightarrow 1} \frac{f(x)-f(1)}{x-1}=\lim\limits _{x \rightarrow 1} \frac{x^{2}-1^{2}}{x-1}=\lim\limits _{x \rightarrow 1} \frac{(x-1)(x+1)}{(x-1)}=\lim\limits _{x \rightarrow 1} x+1=2 \in \mathbb{R}$

خاصية

Soit $ f $ une fonction numérique de courbe $\left(C_{f}\right) $ et de domaine définition $D_{f}$ soit $I \subset D_{f}$ un intervalle ouvert tel que $a$ appartient à l'intérieur de $I$.

Si $f$ est dérivable en $a$

Alors $~\left(C_{f}\right) $ admet une tangente en $A(a, f(a)) $ d'équation cartésienne :

$y=f^{\prime}(a)(x-a)+f(a)$

Dérivabilité à droite et à gauche

تعريف

Soit $f$ une fonction numérique définie sur l'intervalle $ [a, a+\alpha[$ avec $\\ \alpha>0 .$ On dit que la fonction $f$ est dérivable à droite de $a$ s'il existe un nombre réel $l_{d}$ tel que :

$\lim\limits _{x \rightarrow a^{+}} \frac{f(x)-f(a)}{x-a}=\lim\limits _{x \rightarrow a \atop x>a} \frac{f(x)-f(a)}{x-a}=l_{d} \in \mathbb{R}$

Dans ce cas, on appelle $l_{d}$ le nombre dérivé à droite de $f$ en $a$ et on le note $f_{d}^{\prime}(a) $.

تعريف

Soit $f$ une fonction numérique définie sur l'intervalle $] a-\alpha, a] $ avec $\alpha>0 . $ On dit que la fonction $f$ dérivable à gauche de $a, $ s'il existe un nombre réel $l_{g}$ tel que :

$\lim\limits _{x \rightarrow a^{-}} \frac{f(x)-f(a)}{x-a}=\lim\limits _{x \rightarrow a \atop x<a}\frac{f(x)-f(a)}{x-a}=l_{g} \in \mathbb{R}$

Dans ce cas, on appelle $l_{g}$ le nombre dérivé à gauche de $f$ en $a$ et on le note $f_{g}^{\prime}(a) $.

خاصية

Soit $f$ une fonction numérique de domaine définition $D_{f}$, soit $I \subset D_{f}$ un intervalle ouvert tel que $a$ appartient à l'intérieur de $I .$

$f$ est dérivable en $a$ si et seulement si $f$ est dérivable à droite et à gauche de $a$ et :

$f_{d}^{\prime}(a)=f_{g}^{\prime}(a) $.

انتباه

la dérivabilité à droite et à gauche en $a$ de $f$ n'est pas suffisante pour affirmer que $f$ est dérivable en $a$, il faut toujours vérifier l'égalité des deux nombres dérivés.

Interprétation géométrique

Les deux nombres $f_{d}^{\prime}(a) $ et $f_{g}^{\prime}(a) $ sont respectivement des pentes de deux demis tangents à droite et à gauche de $\left(C_{f}\right) $ au point $A(a, f(a)) $.

مثال

On considère la fonction $f(x)=x^{2}$ définie sur $\mathbb{R}$. Alors, $f$ est dérivable à droite au point $A(1,1)$. En effet,

$\begin{aligned}\lim\limits _{x \rightarrow 1^{+}} \frac{f(x)-f(1)}{x-1}&=\lim\limits _{x \rightarrow 1^{+}} \frac{x^{2}-1^{2}}{x-1}\\[0.2cm] &=\lim\limits _{x \rightarrow 1^{+}} \frac{(x-1)(x+1)}{(x-1)}\\[0.2cm]&=\lim\limits _{x \rightarrow 1^{+}} x+1=2 \in \mathbb{R}\end{aligned}$

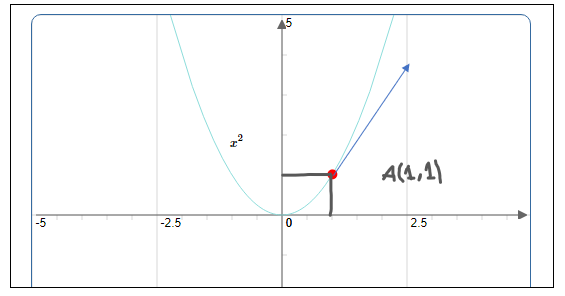
Donc la pente de la tangente ci-dessous : $~~f_{d}^{\prime}(1)=2$

مثال

On considère la fonction $f(x)=x^{2}$ définie sur $\mathbb{R} . $ Alors, $f$ est dérivable à gauche au point $A(1,1) . $ En effet,

$\lim\limits _{x \rightarrow 1^{-}} \frac{f(x)-f(1)}{x-1}=\lim\limits _{x \rightarrow 1^{-}} \frac{x^{2}-1^{2}}{x-1}=\lim\limits _{x \rightarrow 1^{-}} \frac{(x-1)(x+1)}{(x-1)}=\lim\limits _{x \rightarrow 1^{-}} x+1=2 \in \mathbb{R}$

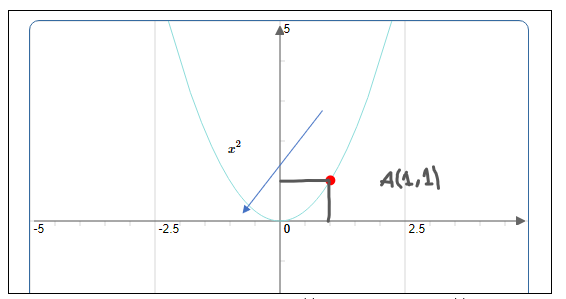
Donc la pente de la tangente ci-dessous : $ f_{g}^{\prime}(1)=2 $

خاصية

Soit $f$ une fonction numérique de domaine définition $D_{f}$, soit $I \subset D_{f}$ un intervalle ouvert tel que $a$ appartient à l'intérieur de $I$.

Si la fonction $f$ est dérivable à droite en $a$, alors la courbe $\left(C_{f}\right) $ admet une demi-tangente au point $A(a, f(a)) $ d'équation cartésienne :

♦ $\left(T_{d}\right): y=f_{d}^{\prime}(a)(x-a)+f(a)~ ;~ ~x \geq a$

Si la fonction $f$ est dérivable à gauche en $a$, alors la courbe $ \left(C_{f}\right) $ admet une demi-tangente au point $A(a, f(a)) $ d'équation cartésienne :

♦ $\left(T_{g}\right): y=f_{g}^{\prime}(a)(x-a)+f(a) ~;~~ x \leq a$

♦ Si $~\lim\limits _{x \rightarrow a^{+}} \frac{f(x)-f(a)}{x-a}=\pm \infty\left(\text { resp. } \lim\limits _{x \rightarrow a^{-}} \frac{f(x)-f(a)}{x-a}=\pm \infty\right) $, alors $f$ n’est pas dérivable à droite (resp. à gauche) en $a$.

Dans ce cas, $\left(C_{f}\right) $ admet une demi- tangente verticale à droite (resp. à gauche ) au point $A(a, f(a)) $.

مثال

1. Tangente parallèle à l’axe des abscisses (horizontal).

La fonction $ f(x)=(x-1)^{2}$ est dérivable en $1$ . En effet,

$\lim\limits _{x \rightarrow 1} \frac{(x-1)^{2}-0}{x-1}=\lim\limits _{x \rightarrow 1} x-1=0$

Donc l’équation de la tangente est : $~~ y=0 \times(x-1)+0=0 $

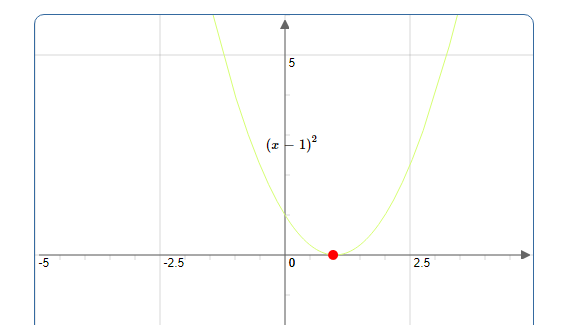
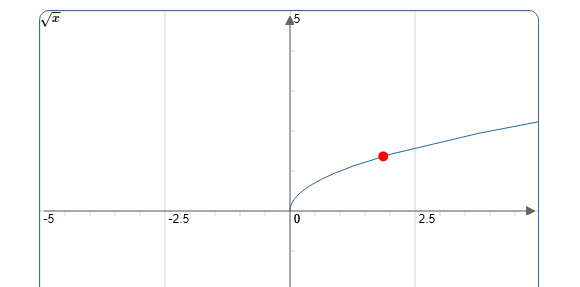
2. Demi-tangente parallèle à l’axe des ordonnées (verticale).

Soit la fonction $~f(x)=\sqrt{x}~$ définie sur $\mathbb{R}^{+} $.

$f$ est bien définie au voisinage de $0$, alors on étudie la dérivabilité à droite $\\$ de $0$ :

$\lim\limits _{x \rightarrow 0^{+}} \frac{\sqrt{x}-\sqrt{0}}{x-0}=\lim\limits _{x \rightarrow 0^{+}} \frac{\sqrt{x}}{x}=\lim\limits _{x \rightarrow 0^{+}} \frac{1}{\sqrt{x}}=\frac{1}{0^{+}}=+\infty$

Donc $ f$ n’est pas dérivable à droite en $ 0 \Rightarrow $ admet une demi-tangente verticale dirigée vers le haut puisque on a « $ 0^{+} $» et « $ +\infty $» (le même signe)

Remarque

L’interprétation géométrique du cas précédent se découle des signes de point de convergence et le résultat de la limite. Généralement, nous avons 4 cas

$\lim\limits _{x \rightarrow a^{\pm}} \frac{f(x)-f(a)}{x-a}=\pm \infty$

حيلة

Les cas possibles	«$$ a^{+} $$» et «$$ +\infty $$ »	«$$ a^{-} $$» et «$$ -\infty $$ »	«$$ a^{+} $$» et «$$ -\infty $$ »	«$$ a^{-} $$» et «$$ +\infty $$ »
Interprétation géométrique	Demi-tangente verticale à droite dirigée vers le haut.	Demi-tangente verticale à gauche dirigée vers le haut.	Demi-tangente verticale à droite dirigée vers le bas.	Demi-tangente verticale à gauche dirigée vers le bas.

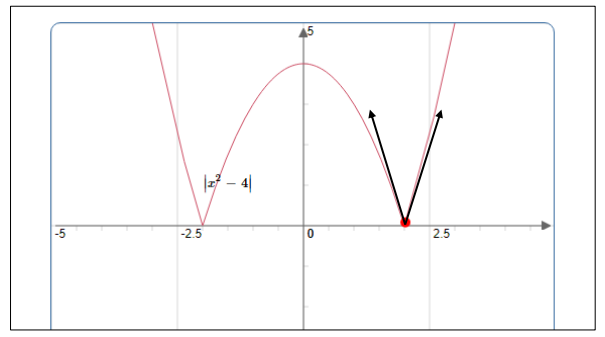
3. Point anguleux : la courbe d’une fonction $ f $ admet un point anguleux en $ a$ si $ f $ est dérivable à droite et à gauche de $ a $ mais $ f_{d}^{\prime}(a) \neq f_{g}^{\prime}(a) $. Par exemple la fonction $~f(x)=\left|x^{2}-4\right|~$ en $2 \\[0.2cm]$ $\lim\limits _{x \rightarrow 2^{+}} \frac{\left|x^{2}-4\right|-0}{x-2}=\lim\limits _{x \rightarrow 2^{+}} \frac{x^{2}-4}{x-2}=\lim\limits _{x \rightarrow 2^{+}} x+2=4 \\[0.2cm]$ $\lim\limits _{x \rightarrow 2^{-}}\frac{\left|x^{2}-4\right|-0}{x-2}=\lim\limits _{x \rightarrow 2^{-}} \frac{-x^{2}+4}{x-2}=\lim\limits _{x \rightarrow 2^{+}}-(x+2)=-4\\[0.2cm]$ Donc,$\quad 4 \neq-4$