-
-
Maths
Les primitives et calcul intégral
2ème année bac Sciences Math A Mathématiques Les primitives et calcul intégral fiche de cours
Les fonctions primitives
Hello guys! Savez vous que le grand physicien Isaac Newton et le grand mathématicien philosophe Gottfried Leibniz sont considérés comme co-inventeurs du calcul différentiel et Intégral.
Êtes-vous prêts les amis à plonger dans le cerveau de ces deux grands scientifiques? $$\\$$ Let's do it! ...
تعريف
Soient $$f$$ et $$F$$ deux fonctions numériques définies sur un intervalle $$I$$ de $$\mathbb{R}.\\$$ On dit que la fonction $$F$$ est une primitive de la fonction $$f$$ sur $$I$$ si: $\\[0.2cm]$
- $$F$$ est dérivable sur $$I$$
- $$(\forall x \in I)\quad F'(x)=f(x)\\[0.2cm]$$
تطبيق
Soit $$F$$ une fonction dérivable sur $$\mathbb{R}$$ telle que: $$F: x \rightarrow \ln(\sqrt{1+x^2}+x) \\$$ On a:
$$\\[0.2cm]F'(x)=(\ln(\sqrt{1+x^2}+x))' = \frac{(\sqrt{1+x^2})'+x'}{\sqrt{1+x^2}+x}= \frac{\frac{x}{\sqrt{1+x^2}}+1}{\sqrt{1+x^2}+x}=\frac{1}{\sqrt{1+x^2}}=f(x)\\[0.2cm]$$
Alors $$F$$ est la fonction primitive de $$f:x \rightarrow \frac{1}{\sqrt{1+x^2}}$$
تطبيق
Trouver la primitive de $$f:x \rightarrow x^2$$ définit sur $$\mathbb{R}$$ telle que: $$G(1)=-1\\[0.2cm]$$ Solution: $$(\forall x \in \mathbb{R})~~~~G(x)=\frac{1}{3}x^3+c \\[0.2cm]$$ On a: $\\ \begin{aligned}G(1)=-1 &\Leftrightarrow \frac{1}{3}1^3+c=-1 \\&\Leftrightarrow c=\frac{-4}{3}\end{aligned}\\[0.2cm]$ D'où: $$(\forall x \in \mathbb{R})~~~~G(x)=\frac{1}{3}x^3-\frac{4}{3}$$
Continuité et fonction primitive
خاصية
Toute fonction continue sur un intervalle $$I$$ admet une primitive définie sur cet intervalle.
Opérations sur les primitives
خاصية
Si $F$ et $G$ sont des primitives des fonctions $f$ et $g$ sur un intervalle $I$, alors $\\ F + G$ est une primitive de $f + g$ sur $I.$ Car:
$$\\[0.2cm](F+G)^{'} = F^{'} + G^{'} = f + g$$
خاصية
Si $F$ est une primitive de la fonction $f$ sur un intervalle $I$ et $c$ est un nombre réel, alors $cF$ est une primitive de $cf$ sur $I$. Car:
$$\\[0.2cm](cF)^{'} = cF^{'} = cf\\[0.2cm]$$
تطبيق
La fonction définie par $$F(x) = \frac{x^{4}}{4}$$ est une primitive sur l'ensemble des nombres réels de la fonction $f$ définie par $$f(x) = x^{3}.\\$$ La fonction définie par $$G(x) =3x$$ est une primitive de la fonction définie par $$g(x) = 3$$ sur $$\mathbb{R}.\\$$ Du coup, une primitive de la fonction $f + g$ sur $$\mathbb{R}$$ est donc $\\$ la fonction $F + G$ définie par $$F(x) + G(x) = \frac{x^{4}}{4}+ 3x$$ sur $$\mathbb{R}$$.
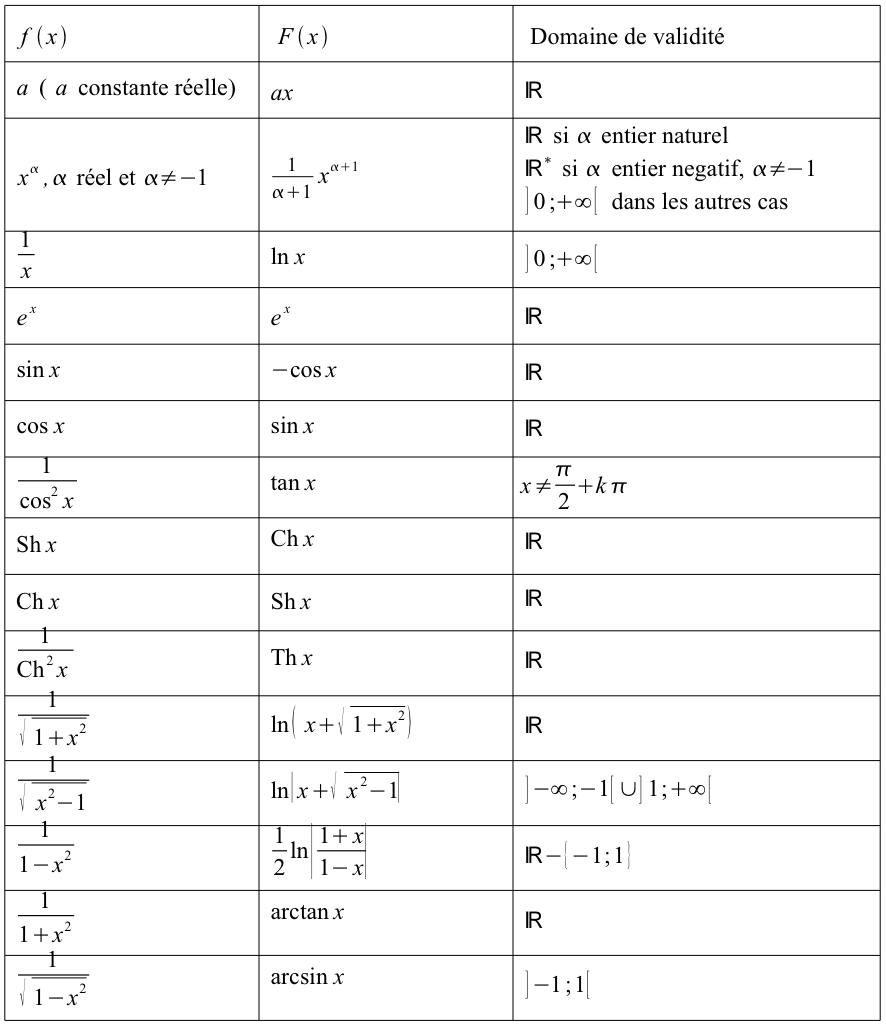
Calcul intégral
Définition et applications
تعريف
Soient $f$ une fonction continue sur l'intervalle $$I$$ et $$a$$, $$b$$ deux éléments de $$I$$. On appelle intégrale de la fonction $$f$$ de $a$ à $b$, le nombre:
$$\\ \int_{a}^{b} f(x) \,dx =[F(x)]^{b}_{a}= F(b)-F(a)\\$$
telle que: $$F$$ est la primitive de $$f$$ sur $$I$$.
ما يجب معرفته
Dans l'écriture $$\int_a^b f(x)\, dx$$, il est possible de remplacer la variable $$x$$ par une autre:
$$\\ \int_a^b f(x)\, dx=\int_a^b f(t)\, dt =\int_a^b f(y) \, dy\\$$
Voyons si vous pouvez comprendre ce même ... 😀 Sachant que $$\frac{d}{dy}$$ est la dérivée d'une fonction par rapport à la variable $y$
تطبيق
$$\int_{0}^{1} \frac{e^x}{1+4e^{2x}} \,dx = [\frac{1}{2} Arctan(2e^x)]_0^1 = \frac{1}{2} Arctan(2e^1)-\frac{1}{2} Arctan(2e^0)$$
خاصية
Soient $f$ et $g$ deux fonctions continues sur $$[a;b]$$, on a:
- $$\\ \int_a^b (f(x)+g(x))\, dx = \int_a^b f(x)\, dx + \int_a^b g(x)\, dx\\[0.2cm]$$
- $$\int_a^b c.f(x)\, dx= c.\int_a^b f(x)\, dx$$ avec $$c$$ une constante
خاصية
RELATION DE CHASLES $$\\$$ Si $f$ est une fonction continue sur un intervalle $$I=[a;b]$$ et $$c \in I$$ , alors :
$$\int_a^b f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx$$
ما يجب معرفته
- $$\int_{a}^{a} f(x) dx = 0\\[0.2cm]$$
- $$\int_a^b f(x) dx = -\int_b^a f(x) dx$$
تطبيق
Calcul des intégrales: $$\\[0.2cm] \begin{aligned} \int_{0}^{1} \frac{x+1}{1+2x} dx &= \int_{0}^{1} \frac{1}{2}.(\frac{2x+1}{2x+1}+\frac{1}{1+2x}) dx \\[0.2cm]&= \frac{1}{2} \int_{0}^{1} (1+ \frac{1}{2}.\frac{(1+2x)^{'}}{1+2x}) dx \\[0.2cm] &= [\frac{1}{2}x+\frac{1}{4}\ln(2x+1)]_{0}^{1} \int_{0}^{1} \frac{1}{1+e^{x}} dx \\[0.2cm]& = \int_{0}^{1} \frac{1+e^{x}-e^{x}}{1+e^{x}} dx \\[0.2cm] &= [x-_ln(1+e^{x})]^{1}_{0}\\[0.2cm] &= 1-\ln(1+e^{1})+\ln(2) \int_0^1 \frac{dx}{1+x^2} \\[0.2cm] &= \int_0^1 \frac{1}{1+x^2} dx \\[0.3cm] &= [\operatorname{Arctan(x)}]_0^1\\[0.2cm] &= \operatorname{Arctan}(1)-\operatorname{Arctan}(0)=\frac{\pi}{4}\end{aligned}$$
تطبيق
$$I=\int_0^\frac{\pi}{2} \cos^2(x) dx$$ et $$ J=\int_0^\frac{\pi}{2} \sin^2(x) dx\\[0.3cm]$$ Calcul de $$I+J$$ et $$I-J\\[0.2cm]$$ -Calculons $$I+J\\[0.2cm]$$ $$\begin{aligned}I+J &= \int_0^\frac{\pi}{2} \cos^2(x) d_{x} + \int_0^\frac{\pi}{2} \sin^2(x) dx\\[0.2cm]&= \int_0^\frac{\pi}{2} (\cos^2(x)+\sin^2(x)dx\\[0.2cm]&= \int_0^\frac{\pi}{2} 1 dx = [x]_0^\frac{\pi}{2}=\frac{\pi}{2}\end{aligned} \\[0.2cm]$$ D'où: $$I+J= \frac{\pi}{2}\\[0.2cm]$$ -Calculons $I-J$ $$\\[0.2cm]\begin{aligned} I-J &= \int_0^\frac{pi}{2} \cos^2(x) dx - \int_0^\frac{\pi}{2} \sin^2(x) dx\\[0.2cm]&= \int_0^\frac{pi}{2} (\cos^2(x)-\sin^2(x))dx\\[0.2cm]&=\int_0^\frac{pi}{2} \cos(2x) dx\\[0.2cm]&=[\frac{1}{2} \sin(2x)]_0^\frac{\pi}{2}\\[0.2cm]&=\frac{1}{2} \sin(\frac{2\pi}{2})-\frac{1}{2}\sin(0)=0 \end{aligned} \\[0.2cm]$$ D'où: $$I-J=0\\[0.2cm]$$ $$\left\{ \begin{array}{lcl} I+J=\frac{\pi}{2}\\ I-J=0 \\ \end{array} \right. \Rightarrow \left\{ \begin{array}{lcl} 2I=\frac{\pi}{2}\\ 2J=\frac{\pi}{2} \\ \end{array} \right.\Rightarrow I=J=\frac{\pi}{4} $$
Expression d'une primitive à l'aide d'une intégrale
نظرية
Soient $$f$$ une fonction continue sur un domaine $$I$$ et $$a$$ un élément de $$I\\$$ La fonction $$\phi$$ définie sur $$I$$ par:
$$\phi (x) = \int_a^x f(t) \,dt$$
est la primitive de $$f$$ sur le domaine $$I$$, s'annulant en $$a.\\$$
تطبيق
Soit $$f$$ la fonction numérique définie par $$f: x \rightarrow \frac{\cos(x)}{x^2+1}\\$$ La primitive de la fonction $$f$$ sur $$\mathbb{R}$$ et qui s'annule en $5$ est:
$$\phi(x)= \int_5^x \frac{\cos(t)}{t^2+1} \,dt.$$
en fait : $$~\phi'(x)=(\int_5^x \frac{\cos (t)}{t^2+1} \,dt)'=\frac{\cos (x)}{x^2+1}=f(x)$$
نظرية
Soient $$f$$ une fonction continue sur un domaine $$I$$ et $$v$$ une fonction dérivable sur un domaine $$E$$ telles que $$v(E) \subset I, $$ alors:
$$(\forall a \in I)~~~~\phi : x \rightarrow \int_a^{v(x)} f(t)\,dt$$
est dérivable sur $$E$$ et on a:
$$(\forall x \in E)~~ \phi'(x)=(\int_a^{v(x)} f(t)\,dt)'=v'(x)f(v(x))$$
تطبيق
$$(\forall x \in \mathbb{R})~~~~H(x)=\int_0^{x^2+2x} \sqrt{1+t} \, dt\\$$ Montrons que $$H$$ est dérivable sur $$\mathbb{R}$$ et calculons $$H'(x)\\$$ On a: $$\\[0.2cm]\left\{ \begin{array}{lcl} v:x \rightarrow x^2+2x~~ , \text{est dérivable sur} \mathbb{R}\\[0.2cm] v(\mathbb{R}) \subset [-1;+\infty[ ~~~~~(\text{car}~(x+1)^2>0, \Rightarrow , x^2+2x>-1)\\[0.2cm] x\rightarrow \sqrt{x+1}~~~\text{est continue sur} ~[-1;+\infty[ \end{array} \right. \\$$ Alors: $$H$$ est dérivable sur $$\mathbb{R}$$ et on a:
Soit $$x \in \mathbb{R} \\[0.2cm]$$ $$\begin{aligned} H'(x)=(\int_0^{x^2+2x} \sqrt{1+t}d_t)'&=(x^2+2x)'\sqrt{1+(x^2+2x)}\\[0.2cm]&=2(x+1)(|x+1|)\end{aligned}$$
ما يجب معرفته
Le cas général :
Soient $$u$$ et $$v$$ deux fonctions dérivables sur $$E$$ telles que $$u(E)\subset I$$ et $$v(E) \subset I$$ et $$f$$ une fonction continue sur $$I\\[0.2cm]$$ Alors la fonction $$\phi:x \rightarrow \int_{u(x)}^{v(x)}f(t)dt $$ est dérivable sur $$E$$ et on a: $$\\[0.2cm] \phi'(x)=(\int_{u(x)}^{v(x)}f(t)dt)'=v'(x)f(v(x))-u'(x).f(u(x))$$
تطبيق
On a: $$(\forall x \in \mathbb{R})~~~F(x)=\int_{\cos(x)}^{\sin(x)}\sqrt{1-t^2} \, dt \\ $$ $$ u: x \rightarrow \cos(x)$$ est dérivable sur $$\mathbb{R}$$ et $$u(\mathbb{R}) \subset [-1;1]\\$$ $$v:x \rightarrow \sin(x)$$ est dérivable sur $$\mathbb{R}$$ et $$v(\mathbb{R}) \subset [-1;1]\\$$ $$x \rightarrow \sqrt{1-x^2}$$ est continue sur $$[-1;1]\\$$ Alors la fonction $$F$$ est dérivable sur $$\mathbb{R}\\$$ Soit $$x$$ un élément de $$\mathbb{R}\\[0.2cm]$$ $$F'(x)=(\int_{\cos(x)}^{\sin(x)}\sqrt{1-t^2} \, dt)'\\$$ $$\hspace{1cm}=\sin'(x)\sqrt{1-\sin^2(x)}-\cos'(x)\sqrt{1-\cos^2(x)}\\$$ $$\hspace{1cm}=\cos(x)\sqrt{\cos^2(x)}+\sin(x)\sqrt{\sin^2(x)}\\$$ $$\hspace{1cm}=\cos(x).|\cos(x)|-\sin(x)|\sin(x)|$$
Techniques de calcul d'intégrales
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو
- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي
Signaler une erreur