Calcul vectoriel dans le plan

Vecteurs du plan ( Rappel ) 

Activité

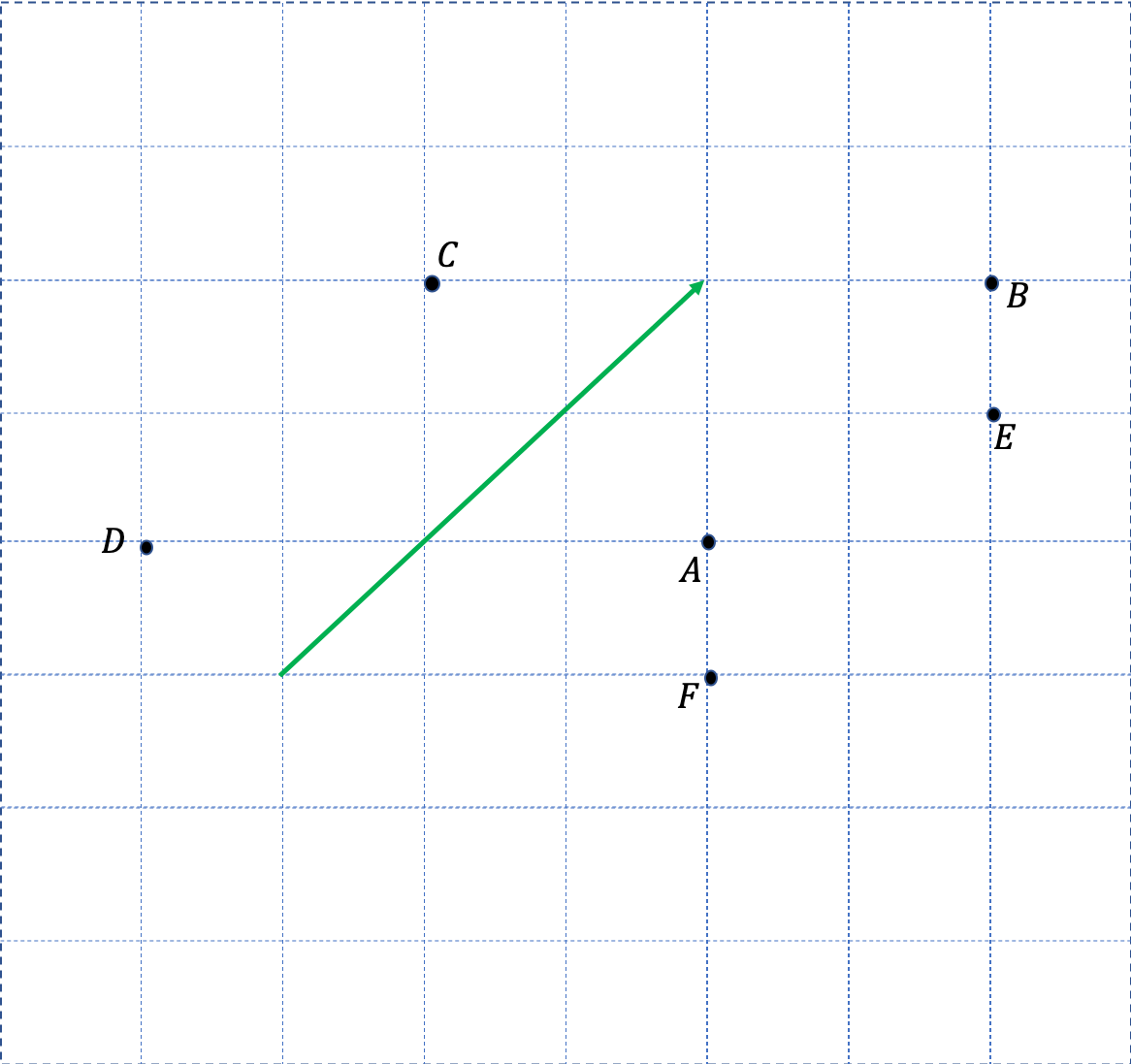
Dans le plan $(P)$, on considère le vecteur $\overrightarrow{AB}$.

Qu'appelle-t-on ?

• La droite $(AB)$ pour le vecteur $\overrightarrow{AB}$ ?
• Pour le vecteur  $\overrightarrow{AB}$ si on part de $A$ vers $B$.
• La distance $AB$ pour le vecteur $\overrightarrow{AB}$

Que peut-on dire : 

• Des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ ?

Réponses : 

• La droite $(AB)$ représente la direction du vecteur $\overrightarrow{AB}$.
• On appelle le sens du vecteur $\overrightarrow{AB}$ le sens de la demi-droite $[AB)$
• La longueur ou norme de $\overrightarrow{AB}$, notée $||\overrightarrow{AB}||=AB$ représente également la distance de A à B
• Les vecteurs $\overrightarrow{DC}$ et $\overrightarrow{AB}$ sont égaux ( même norme , même sens et directions parallèles).

Autres rappels : 

• Un vecteur unitaire est un vecteur de longueur 1. Soit $\overrightarrow{AB}$ un vecteur non nul, alors il a seulement deux vecteurs unitaires qui sont $\overrightarrow{u} = \frac{1}{AB} \overrightarrow{AB}$ et $\overrightarrow{v} = -\frac{1}{AB} \overrightarrow{AB}$
• Cas particulier : $A=B$, le vecteur $\overrightarrow{AA} = \overrightarrow{0}$ le vecteur nul. Il n'a pas direction, pas de sens et a pour longueur 0.
• Deux vecteurs non nuls sont égaux si et seulement si : ils ont même direction et même sens et même longueur.
• (ABCD) est un parallélogramme si et seulement si :$\overrightarrow{AB} = \overrightarrow{DC}$

Opérations dans l'ensemble des vecteurs du plan :

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني