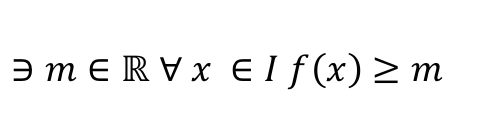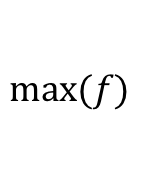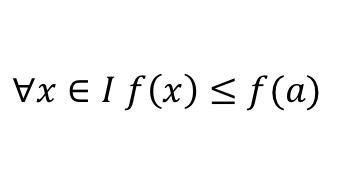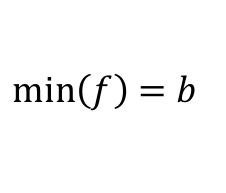الدوال المكبورة ، المصغورة و المحدودة
الدوال المكبورة
دالة مكبورة
لتكن f دالة عددية
نقول أن الدالة f مكبورة في مجال I إذا و فقط إذا :
يعني يوجد عدد حقيقي M بحيث الدالة تكون دائما أصغر من أو تساوي هذا العدد في المجال I
بعض الأمثلة :
- الدالة sin مكبورة بالعدد 1 في المجال R بالفعل، نعلم أن
و بالتالي فإن الدالة sin مكبورة في R
- الدالة
مكبورة بالعدد
في المجال
بالفعل، لدينا
إذا
الدوال المصغورة
لتكن f دالة عددية
نقول أن الدالة f مصغورة في مجال I إذا و فقط إذا :
يعني يوجد عدد حقيقي m بحيث الدالة تكون دائما أكبر من أو تساوي هذا العدد في المجال I
الدوال المحدودة
تكون دالة عددية محدودة إذا كانت مكبورة و مصغورة
الدوال الدورية
ما هي الدوال الدورية ؟
لتكن f دالة معرفة على
ليكن T عدد حقيقي
نقول أن f دالة دورية دورها T لما :
بعض الأمثلة
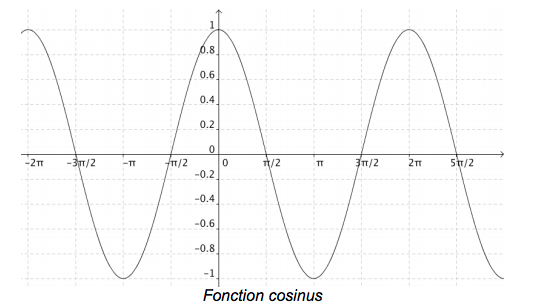
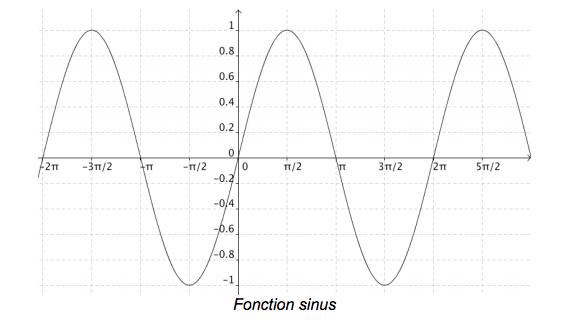
- الدوال المثلثية sin و cos دوال دورية دورها
نلاحظ أن قيمة الدالة cos تبقى ثابتة إذا أضفنا كما يوضح الشكل أعلاه
مطاريف دالة عددية
مفهوم مطاريف دالة عددية يعود فقط إلى شرح مفهومي القيمة القصوى و القيمة الدنيا لدالة معينة :
القيمة القصوى لدالة
- القيمة القصوى لدالة f على مجال I هي أكبر قيمة للدالة على هذا المجال
- القيمة القصوى للدالة f يرمز له كذلك ب
- بما أن القيمة القصوى هي أكبر قيمة للدالة f في المجال I ، فيوجد عدد حقيقي a بحيث
و بالتالي يكون لدينا :
- و تكون بذلك
هي القيمة القصوى للدالة f في المجال I
- لما يكون لدينا جدول تغيرات الدالة ، يصبح من السهل تحديد القيمة القصوى
مثال :
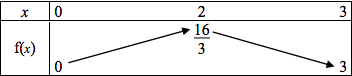
لنأخذ دالة f ذات جدول التغيرات أسفله :
من الواضح أن القيمة القصوى للدالة f هو العدد 16/3 و هو صورة العدد 2
القيمة الدنيا لدالة
- القيمة الدنيا لدالة f على مجال I هي أصغر قيمة للدالة على هذا المجال
- القيمة القصوى للدالة f يرمز له كذلك ب
- بما أن القيمة الدنيا هي أصغر قيمة للدالة f في المجال I ، فيوجد عدد حقيقي b بحيث
و بالتالي يكون لدينا :
- و تكون بذلك
هي القيمة الدنيا للدالة f في المجال I
- لما يكون لدينا جدول تغيرات الدالة ، يصبح من السهل تحديد القيمة الدنيا
مثال :
لنأخذ دالة f ذات جدول التغيرات أسفله :
من الواضح أن القيمةالدنيا للدالة f هو العدد 3 و هو صورة العدد 3 على المجال
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي
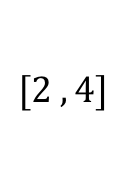 بالفعل، لدينا
بالفعل، لدينا 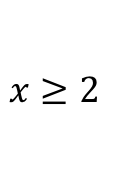 إذا
إذا