Fiche de cours

En mathématique, les vecteurs sont des objets que nous pouvons tracer géométriquement grâce à leurs propriétés (origine, direction, sens et norme). En plus, le vecteur constitue un élément important et le pilier de la branche mathématique : l’algèbre linéaire, par l’addition et la multiplication par des scalaires nous obtenons des résultats pertinents à titre d’exemple la relation de Chasles.

En physique classique ou moderne, le vecteur est un moyen efficace pour présenter des grandeurs tels que : la vitesse, la quantité de mouvement, la force, le moment ... alors nous appelons ces grandeurs physiques par : Grandeurs Vectorielles.

Ce cours se focalisera sur la notion de vecteur dans l’espace comme un complément de tout ce qu’a vu en tronc commun dans le plan. Alors, nous ferons une transition vers l’espace et ajouter une dimension à notre étude mathématique.

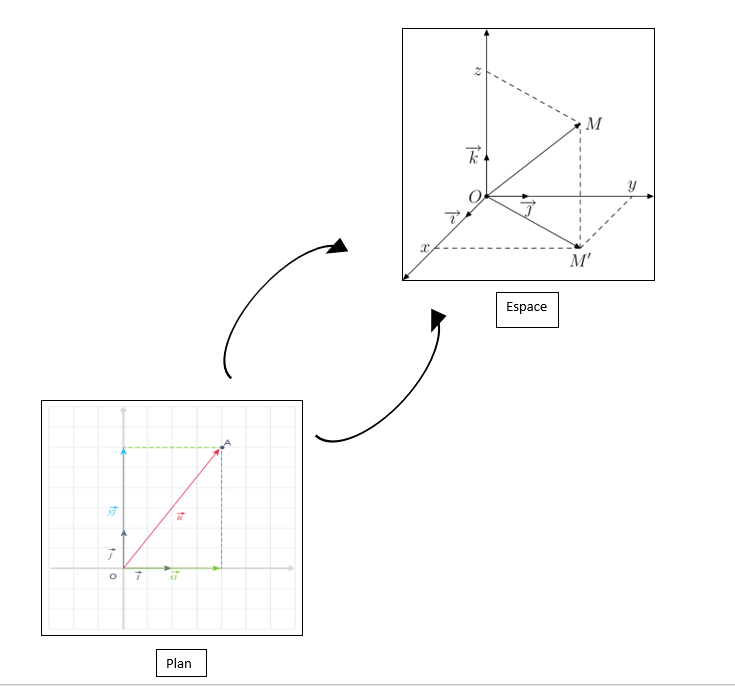
Notion de vecteur dans l’espace

Extension d’un vecteur

Rappel :

Soient $A$ et $B$ deux points dans un repère orthonormé $(O, \vec{\imath}, \vec{\jmath})$ . Le vecteur $ \overrightarrow{A B}$  se caractérise par les éléments suivants : 

  • L’origine : le point de commencent du vecteur, dans ce cas c'est $$A $$
  • La direction : la droite $$ (A B) $$
  • Le sens : est déterminé par la flèche au-dessus de vecteur, dans ce cas de $A$ à $$B $$
  • La norme : correspondant à longueur du vecteur, c’est une grandeur qui toujours positif. $\\$ On écrit $\|\overrightarrow{A B}\|=A B $

Alors, toutes ces notions sont prolongeables à l’espace, ainsi que toutes les propriétés dans le plan restent valables dans l’espace.

مثال

Représentation graphique 

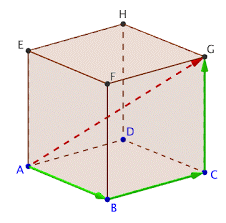
La figure ci-dessus illustre la propriété de Chasles dans l’espace :

$$\overrightarrow{A G}=\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C G}$$

image/svg+xml Remarque

  • Deux vecteurs sont égaux si et seulement s’ils ont la même direction (ou deux direction parallèles), le même sens et la même norme.$\\[0.2cm]$
  • $$ \overrightarrow{A B}=\overrightarrow{C D} \Leftrightarrow A B D C ~$$  est un parallélogramme  $\\[0.2cm]$
  • Si $~A=B~$  alors le vecteur $\overrightarrow{A B}=\overrightarrow{A A}=\overrightarrow{0}$ est nul. $\\[0.2cm]$
  • $I ~$ est le milieu de $[A B] ~: ~2 \overrightarrow{A I}=\overrightarrow{A B}$ $\\[0.2cm]$
  • On note l'ensemble des vecteurs dans l'espace par $$ V_{3} $$

Les opérations sur les vecteurs dans l’espace

Les vecteurs de l'espace suivent les mêmes règles de construction et de calcul qu'en géométrie plane : l’addition, multiplication par un salaire, Relation de Chasles, propriétés en rapport avec la colinéarité, … restent valides

L’addition :

Soient $$\vec{u}, \vec{v}$$ et $$\vec{w}$$ trois vecteurs de l'espace tels que : $$\left\{\begin{array}{l}\vec{u}=\overrightarrow{O A} \\ \vec{v}=\overrightarrow{O B} \\ \vec{w}=\overrightarrow{O C}\end{array}\right. \\[0.2cm]$$ avec $$A, B$$ et $$C$$ sont des points dans le repère orthonormé $$ (O, \vec{\imath}, \vec{\jmath}, \vec{k}) . \\[0.2cm]$$ Alors $$\vec{w}$$ est le vecteur somme de $$\vec{u}$$ et $$\vec{v} \mathrm{~s}^{\prime} \mathrm{il}$$ vérifie la relation $$: \vec{w}=\vec{u}+\vec{v}$$, autrement $$\overrightarrow{O C}=\overrightarrow{O A}+\overrightarrow{O B}\\[0.2cm]$$ et cela revient à dire que $$O A C B$$ est un parallélogramme.

Interprétation graphique :

  • Si les trois vecteurs n’ont pas la même origine :

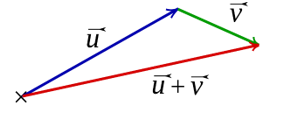
  • Sinon :

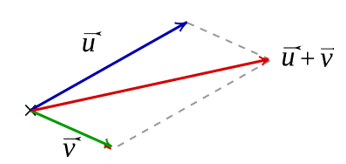
خاصية

Les propriétés de l’addition :

  • Commutativité : soient $$\vec{u}, \vec{v}$$ deux vecteurs de l'espace, $\\[0.2cm]$ alors : $$\quad \vec{u}+\vec{v}=\vec{v}+\vec{u} \\[0.2cm]$$
  • Associativité : soient $$\vec{u}, \vec{v}$$ et $$\vec{w}$$ trois vecteurs de l'espace,$\\[0.2cm]$ alors $$\quad (\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w}) \\[0.2cm]$$
  • L’élément neutre : soit $$\vec{u}$$ un vecteur de l'espace alors, $\\[0.2cm]$ $$\overrightarrow{0}$$ est un élément neutre $$\quad \vec{u}+\overrightarrow{0}=\overrightarrow{0}+\vec{u}=\vec{u} $$

La multiplication par un scalaire :

Soit $$\vec{u}$$ un vecteur non nul de l'espace et soit $$k$$ un scalaire non nul $$\left(k \in \mathbb{R}^{*}\right) . $$

On suppose que $$\vec{u}=\overrightarrow{A B}$$ dans un repère orthonormé $$ (O, \vec{\imath}, \vec{\jmath}, \vec{k}) . $$

Alors, il existe un point $$M$$ sur la droite $$ (A B) $$ tel que, $$\overrightarrow{A M}=k \overrightarrow{A B}$$

Donc, le vecteur $$\vec{p}=\overrightarrow{A M}$$ est nommé le produit de $$\vec{u}$$ par le scalaire $$k$$

Interprétation graphique

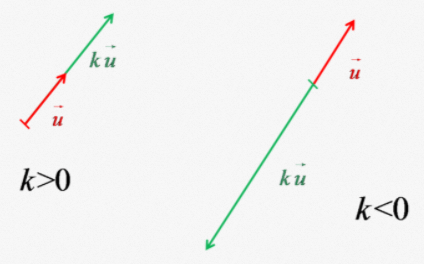
Alors le vecteur $~\vec{p}=k \vec{u}~$ a la même direction que $\vec{u},$ mais le sens dépend du signe de $k :\\[0.2cm]$

  • Si $k>0~$ alors $\vec{p}$ et $\vec{u}$ ayant le même sens.$\\[0.2cm]$
  • Si $k<0 ~$ alors $\vec{p}$ et $\vec{u}$ ayant des signes opposés. $\\[0.2cm]$

En plus, on a la relation suivante :$\quad \|\vec{p}\|=|k|\|\vec{u}\| $

خاصية

  • Pour tout vecteur $\vec{u},~$ $\vec{u} \times 0=\overrightarrow{0} ~$ et pour tout scalaire $~\overrightarrow{0} \times k=\overrightarrow{0} \\[0.2cm]$
  • Soient $\vec{u}$ et $\vec{v} $ deux vecteurs, soient $a$ et $b$ deux scalaires. Alors: $\\[0.2cm]$

$$ \begin{gathered}(a+b) \vec{u}=a \vec{u}+b \vec{u} \\[0.2cm] a(\vec{u}+\vec{v})=a \vec{u}+a \vec{v} \\[0.2cm] a \times(b \vec{u})=b \times(a \vec{u})=(a \times b) \vec{u} \\[0.2cm]1 \times \vec{u}=\vec{u}\end{gathered}\\[0.2cm]$$

  • Soient $\vec{u}$ un vecteur dans l'espace et $k$  un scalaire :$\\[0.2cm]$ $k \times \vec{u}=0 \quad \Leftrightarrow k=0 \quad\text { ou } \quad\vec{u}=\overrightarrow{0}$

مثال

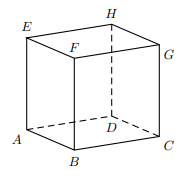
On considère un cube $$ A B C D E F G H .$$

1.a. Simplifier le vecteur $$~\overrightarrow{A C}+\overrightarrow{A E} $$

b. En déduire que $$~\overrightarrow{A G} \cdot \overrightarrow{B D}=0 . $$

c. On admet que $~ \overrightarrow{A G} \cdot \overrightarrow{B E}=0 \\$ Démontrer que la droite $(A G)$  est orthogonale au plan $(B D E)$ 

Corrigé :

1. a) Simplifier le vecteur $\overrightarrow{A C}+\overrightarrow{A E} $

$ \overrightarrow{A C}+\overrightarrow{A E}=\overrightarrow{A C}+\overrightarrow{C G}=\overrightarrow{A G}$

b) En déduire que $\overrightarrow{A G} \cdot \overrightarrow{B D}=0$

$$\overrightarrow{A G} \cdot \overrightarrow{B D}=(\overrightarrow{A C}+\overrightarrow{A E}) \cdot \overrightarrow{B D}=\overrightarrow{A C} \cdot \overrightarrow{B D}+\overrightarrow{A E} \cdot \overrightarrow{B D} $$

$$ [A C] $$ et $[B D]$ sont les diagonales du carré $$A B C D$$ et donc $$\overrightarrow{A C} \cdot \overrightarrow{B D}=0$$

En plus, La droite $$(A E)$$ est perpendiculaire aux droites $$(A B) $$ et $$ (A D) $$ qui sont deux droites sécantes du plan $$ (A B D) $$.

Donc, La droite $$ (A E) $$ est perpendiculaire au plan $$ (A B D) . $$

Cela revient à dire que $(AE)$ est perpendiculaire à toute droite du plan $$ (A B D) $$.

Alors,

$$ (A E) $$ est perpendiculaire à $$(B D) \Rightarrow \overrightarrow{A E} \cdot \overrightarrow{B D}=0$$

D'où

$$ \overrightarrow{A G} \cdot \overrightarrow{B D}=0 $$

c) On admet que $\overrightarrow{A G} \cdot \overrightarrow{B E}=0 .\\[0.2cm]$ Démontrer que la droite $(A G)$ est orthogonale au plan$$ (BDE) $$

La droite $$ (A G) $$ est orthogonale aux droites $$ (B D) $$ et $$ (B E) $$ qui sont deux droites sécantes du plan (BDE). Donc, La droite $$ (A G)$$ est orthogonale au plan $$(B D E)$$.

Vidéo Définitions, Caractértistiques et opérations
15 min
Voir la vidéo

Les propriétés des vecteurs dans l’espace

Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

Version gratuite de Kezakoo
  • Fiches de cours illimitées
  • Une vidéo gratuite par leçon
  • 2 exercices gratuits par leçon
  • Un test gratuit par leçon
S'inscrire gratuitement
Signaler une erreur
Vecteur dans l’espace
Sommaire du cours
Signaler une erreur