Mouvement de rotation d’un solide autour d’un axe fixe

Solide en mouvement de rotation

Les caractéristiques du mouvement rotationnel

Tous les points du solide situés sur l’axe de rotation sont immobiles tous les autres points du solide décrivent des arcs de cercle centrés sur l’axe de rotation. Donc chaque point d’un solide en rotation autour d’un axe fixe a une trajectoire circulaire.

Abscisse angulaire et abscisse curviligne

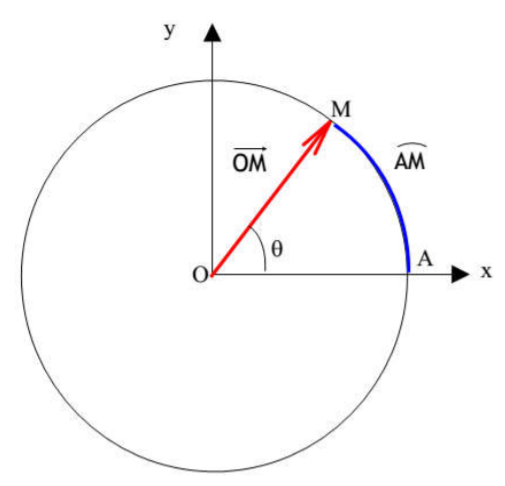
Abscisse angulaire

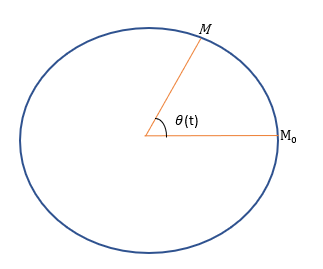
On peut aussi repérer la position du mobile sur le cercle trajectoire par la donnée de l'angle θ(t) orienté au centre du cercle : $$\theta(\mathrm{t})=\left(O \widehat{M_{0} ; O M}\right)$$, l’unité de l’abscisse angulaire est le radian (rad)

Abscisse curviligne

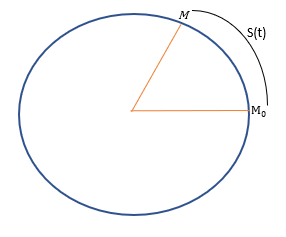
Soit M un point quelconque choisi sur le cercle trajectoire. On oriente la trajectoire dans un sens arbitraire, la position du mobile est repérée par son abscisse curviligne : $$\mathrm{s}(\mathrm{t})=\widehat{\mathrm{M}_{0} \mathrm{M}}$$, l’unité de l’abscisse curviligne est le mètre (m)

Relation entre abscisse curviligne et abscisse angulaire

Il existe une relation géométrique simple entre abscisse curviligne et abscisse angulaire : $$s(t)=R . \theta(t)$$ tel que R le rayon de la trajectoire circulaire

Vitesse angulaire et vitesse linéaire

Vitesse angulaire

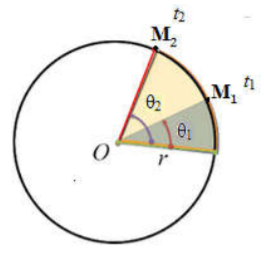
Vitesse angulaire Moyenne

Soit M un point du solide décrit un mouvement circulaire centré sur l’axe ($$\Delta$$) de centre O
- à l’instant $$\mathrm{t}_{1}$$ la position du point M est noté $$\mathrm{M}_{1}$$
- à l’instant $$\mathrm{t}_{2}$$ la position du point M est noté $$\mathrm{M}_{2}$$
Au cours de la durée $$\Delta \mathrm{t}=\mathrm{t}_{2}-\mathrm{t}_{1}$$ le point M parcours l’arc $$\widehat{M_{1} M_{2}}$$ et le solide tourne d’un angle $$\Delta \theta=\theta_{2}-\theta_{1}$$
On appelle vitesse angulaire moyenne le quotient de l'angle $$\theta_{2}-\theta_{1}$$ dont a tourné le point M par le temps $$\mathrm{t}_{2}-\mathrm{t}_{1}$$ mis pour effectuer cette rotation Par définition la vitesse angulaire moyenne du point M est donnée par la relation :
$$\dot{\theta}=\frac{\theta_{2}-\theta_{1}}{t_{2}-t_{1}}$$
Unité de la vitesse angulaire dans SI : rad/s

Vitesse angulaire instantané

La vitesse angulaire instantanée d'un solide à la date t se définit comme la vitesse angulaire moyenne du solide pendant une brève durée autour de la date t.
$$\dot{\theta}=\frac{\theta_{2}-\theta_{1}}{t_{2}-t_{1}}=\frac{\Delta \theta}{\Delta t}$$
La vitesse angulaire \omega est la même pour tous les points du solide en rotation et qui est donc la vitesse angulaire du solide en rotation

Vitesse linéaire

La vitesse linéaire du point M à l’instant t est le quotient de la longueur de l’arc $$\widehat{M_{1} M_{2}}$$ de son parcours par la durée Δt correspondante :
$$v_{\mathrm{t}}=\frac{\mathrm{M}_{1} \mathrm{M}_{2}}{\mathrm{t}_{2}-\mathrm{t}_{1}}$$

انتباه

Si $$\Delta t$$ est grand, on a les vitesses moyennes, si $$\Delta t$$ est petit on a les vitesses instantanées.

Relation entre la vitesse linéaire et la vitesse angulaire

Pour un point M d’un solide en rotation autour d’un axe fixe, situé à une distance r de l’axe de rotation, la distance parcourue pendant une durée $$\Delta \mathrm{t}=\mathrm{t}_{2}-\mathrm{t}_{1}$$ est $$\mathrm{M}_{1} \mathrm{M}_{2}$$ avec $$\Delta \mathrm{s}=\mathrm{M}_{1} \mathrm{M}_{2}=\mathrm{r} \cdot \Delta \theta$$
On a
$$v_{\mathrm{t}}=\frac{\mathrm{M}_{1} \mathrm{M}_{2}}{\mathrm{t}_{2}-\mathrm{t}_{1}}=\frac{\mathrm{r} \cdot \Delta \theta}{\mathrm{t}_{2}-\mathrm{t}_{1}}=\mathrm{r} \cdot \frac{\Delta \theta}{\Delta \mathrm{t}}$$
Et comme $$\frac{\Delta \theta}{\Delta \mathrm{t}}=\dot{\theta} \text { alors } v=\mathrm{r} \cdot \dot{\theta}$$

Accélération angulaire

Le vecteur accélération dans la base de Frenet
$$\overrightarrow{\mathrm{a}}=\mathrm{a}_{\mathrm{t}} \overrightarrow{\mathrm{u}}+\mathrm{a}_{\mathrm{n}} \overrightarrow{\mathrm{n}}=\frac{d \mathrm{v}}{d \mathrm{t}} \overrightarrow{\mathrm{u}}+\frac{\mathrm{v}^{2}}{\mathrm{r}} \overrightarrow{\mathrm{n}}$$
Avec
$$\mathrm{a}_{\mathrm{t}}=\frac{d \mathrm{v}}{d \mathrm{t}} \text { et } v=\mathrm{r} \cdot \dot{\theta} \text { Alors } \mathrm{a}_{\mathrm{t}}=\frac{d(\mathrm{R} \cdot \dot{\theta})}{d \mathrm{t}} \text { donc } \mathrm{a}_{\mathrm{t}}=\mathrm{r} \cdot \frac{d(\dot{\theta})}{d \mathrm{t}}=\mathrm{r} \cdot \ddot{\theta}$$
$$\mathrm{a}_{\mathrm{n}}=\frac{\mathrm{v}^{2}}{\mathrm{r}} \text { et } \mathrm{v}=\mathrm{r} . \dot{\theta} \text { Alors } \mathrm{a}_{\mathrm{n}}=\frac{(\mathrm{r} \cdot \dot{\theta})^{2}}{\mathrm{r}} \text { donc } \mathrm{a}_{\mathrm{n}}=\mathrm{r} . \ddot{\theta}^{2}$$

Relation fondamentale de la dynamique