-
-
Maths
Généralités sur les fonctions
1ère année bac Sciences Maths Maths Généralités sur les fonctions fiche de cours
Le terme « fonction » revient à décrire une relation existante entre deux ensembles de nombres. Concrètement, la fonction est une machine mathématique qui transforme un nombre à une autre dans certaine logique (double, tribale, racine, quotient…). Nous présentons les figures ci-dessous illustrant cette définition :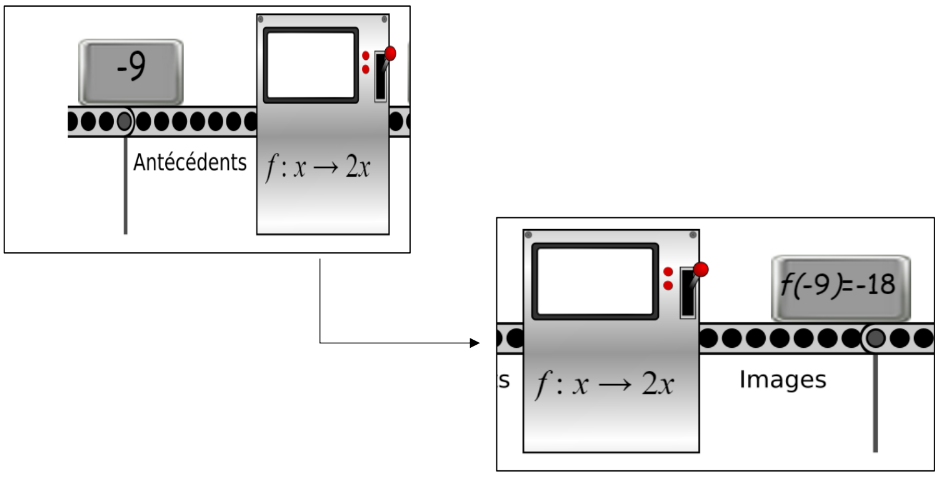 
Donc, nous avons toujours deux ensembles : ensemble de départ et ensemble d’arrivée et la fonction c’est le lien mathématique entre les deux ensembles.
تطبيق
La fonction : $ f(x)=2 x\\$ L’élément de l’entrée : $-9\\$ Le résultat : $-18$
Notion de fonction numérique : Définitions et propriétés
Notion de fonction et Domaine de Définition
تعريف
La fonction $f$ est un procédé qui à chaque nombre $x$ appartenant à l’ensemble $ D_{f} $ associe un nombre $ f(x) \in F. $
On note :
$\begin{aligned} f :~ D_{f} &\rightarrow F\\ x &\rightarrow f(x)\end{aligned}$
On dit que $~ f(x)$ est l'image de $x$ par la fonction $f$.
On dit que $x$ est l'antécédent de $f(x)$ par la fonction $f$.
تعريف
Le domaine de définition d’une fonction $f $ est l’ensemble de nombres réels qui possèdent une image calculable par cette fonction. On note $ D_{f} $ l’ensemble de définition de la fonction $f$.
تطبيق
$\begin{aligned} \text{1-} ~f: D_{f} &\mapsto F\\x &\mapsto x^{2}+x+1 \end{aligned}\\$
est une fonction dite polynomiale avec $~D_{f}=\mathbb{R}\\[0.3cm]$ 2- $g(x)=\frac{2 x}{x-1}\quad$ est une fonction sous forme d'une fraction $\\$ avec $D_{g}=\mathbb{R} \backslash\{1\}\\[0.2cm]$ En effet, $g$ est bien défini si et seulement si le dominateur est non nul . $\\$ Donc $ D_{g}=\{x \in \mathbb{R}~ / ~x-1 \neq 0\}=\{x \in \mathbb{R} ~ / ~x \neq 1\}$ d'où le résultat . $\\[0.3cm]$ 3- $h(x)=\frac{1}{\sqrt{2 x+1}} \quad $ est une fonction irrationnelle avec $D_{h}= ]\frac{-1}{2},+\infty]$ $\\$
En effet, $ h$ est bien défini si et seulement $ \sqrt{2 x+1} \neq 0~$ et $ ~2 x+1 \geq 0\\[0.2cm]$ Donc
$\begin{aligned}D_{h} &=\{x \in \mathbb{R} / \sqrt{2 x+1} \neq 0 \}~~\text{et}~~2 x+1 \geq 0 \\[0.2cm]& ={x \in \mathbb{R}~/ ~2 x+1 \neq 0 ~~\text{et} ~~2 x+1 \geq 0} \\[0.2cm]& \left.={x \in \mathbb{R}~~ / ~~2 x+1>0}\\= ]\frac{-1}{2},+\infty\right.[\end{aligned}$
ما يجب معرفته
- Pour toutes les fonctions polynomiales $ D_{f}=\mathbb{R}\\[0.2cm]$
- Pour les fonctions de type $\frac{Q(x)}{P(x)} : \quad D_{f}=\{x \in \mathbb{R} / P(x) \neq 0\}\\[0.2cm]$
- Pour les fonctions de type $ \sqrt{P(x)} : \quad D_{f}=\{x \in \mathbb{R} / P(x) \geq 0\}$
Représentation graphique d’une fonction
La représentation graphique ou courbe d'une fonction est l'ensemble, noté $\left(C_{f}\right),$ des points $M(x, f(x))~$ tel que $x\in D_{f} .$
On écrit $\quad \left(C_f\right)=\left\{M(x, f(x)) ~/ ~x \in D_{f}\right\}$.
تطبيق
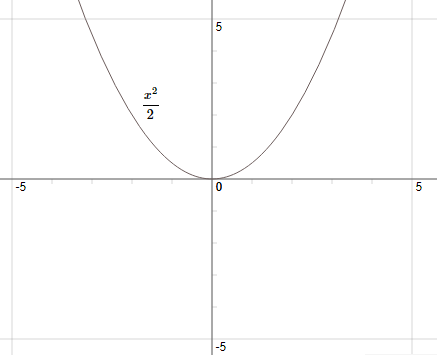
1- La représentation graphique de la fonction $f(x)=2 x $ est une droite passant par l’origine. $\\[0.2cm]$ 2- La représentation graphique de la fonction $ g(x)=\frac{x^{2}}{2}$ est une parabole
3- La représentation graphique de $ ~h(x)=\frac{2 x-1}{\sqrt{x^{2}+1}} $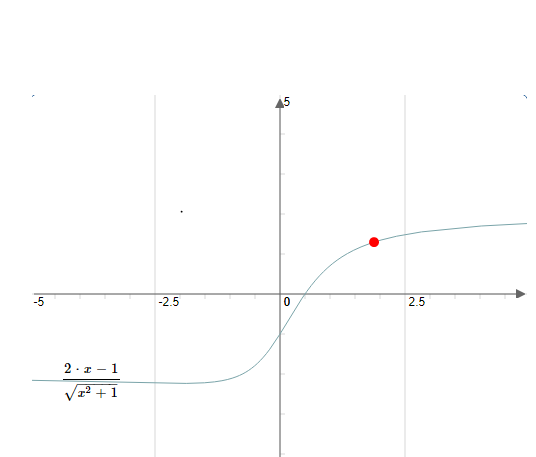 
La parité
Fonction paire
تعريف
Une fonction $f $ de domaine de définition $D_{f}$ est paire si et seulement si $\\$ pour tout $ x \in D_{f} $ :
- $-x \in D_{f} $
- $f(-x)=f(x)$
خاصية
Une fonction $f$ est paire si et seulement si sa courbe est symétrique par rapport à l’axe des ordonnées.
تطبيق
$ f(x)=x^{2} $: $\\$ En utilisant la définition , $~D_{f}=\mathbb{R} $ car $ f $ est polynomiale. $\\$ Soit $ x \in \mathbb{R} $ alors évidement $-x \in \mathbb{R} \\$ Alors ,$ ~f(x)=(-x)^{2}=x^{2}=f(x) $
d'où la fonction est paire .$\\$
Graphiquement, la fonction est symétrique par rapport à l’axe des ordonnées comme l’illustre la figure ci-dessous :$\\$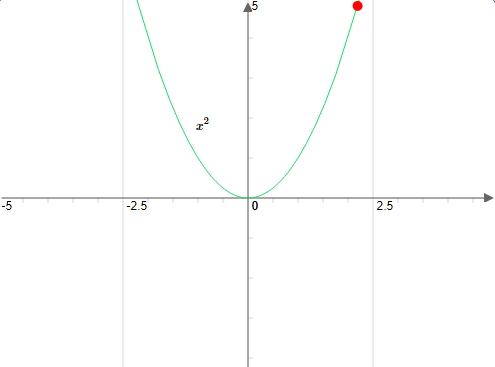 
La fonction impaire
تعريف
Une fonction $f$ de domaine de définition $D_{f}$ est impaire si et seulement si $\\$ pour tout $ x \in D_{f}$ :
- $ -x \in D_{f} $
- $ f(-x)=-f(x) $
خاصية
Une fonction $f$ est paire si et seulement si sa courbe est symétrique par rapport à l’origine du repère.
تطبيق
$ f(x)=x^{3} : \\$ En utilisant la définition, $D_{f}=\mathbb{R}$ car $ f $ est polynomiale. $\\$ Soit $ x \in \mathbb{R}~ $ alors évidement $-x \in \mathbb{R} \\$
Alors, $~ f(-x)=(-x)^{3}=-x^{3}=-f(x)$ d'où la fonction est impaire. $\\$
Graphiquement, la fonction est symétrique par rapport à l’origine du repère comme l’illustre la figure ci-dessous : $\\$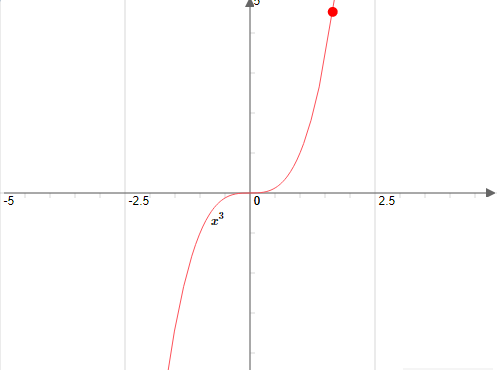 
La fonction majorée, minorée, bornée
تعريف
Soit $f$ une fonction numérique de domaine définition $D_{f}$, soit $m$ et $M$ deux réels. Alors,
$\bullet$ $f $ est majorée par $ ~M \Leftrightarrow \forall x \in D_{f} ,~ f(x) \leq M \\[0.2cm]$
$\bullet$ $f$ est minorée par $ ~m \Leftrightarrow \forall x \in D_{f} , ~f(x) \geq m \\[0.2cm] $
$\begin{aligned} \bullet~ f ~\text{est bornée} ~&\Leftrightarrow ~f~ \text{est majorée et minorée}\\ ~&\Leftrightarrow \forall x \in D_{f}, ~m \leq f(x) \leq M \end{aligned}$
ما يجب معرفته
Parfois le nombre $m$ ou $M$ n’est pas donné explicitement, c’est aux étudiants de le déterminer, dans ce cas la définition est :
$\bullet$ $f $ est majorée $\Leftrightarrow \exists ~M \in \mathbb{R}, ~\forall x \in D_{f}, ~f(x) \leq M \\[0.2cm]$
$\bullet$ $ f $ est minorée $\Leftrightarrow \exists ~m \in \mathbb{R}, ~\forall x \in D_{f}, ~f(x) \geq m \\[0.2cm]$
$\begin{aligned} \bullet ~ f ~\text{est bornée}~ &\Leftrightarrow f ~\text{est majorée et minorée} \\ &\Leftrightarrow \exists ~(m, M) \in {\mathbb{R}} \times {\mathbb{R}} , ~\forall {x} \in {D}_{f},~m \leq f(x) \leq M \end{aligned}$
تطبيق
1- $f(x)=x^{2}$ est minorée par $0$ car $~\forall x \in \mathbb{R} , ~x^{2} \geq 0 \\[0.3cm]$ 2- Soit $ g $ la fonction définie sur $[1,+\infty[~$ par $~g(x)=\frac{1}{x} \\[0.2cm]$ Alors, $g $ est majorée par $ 1$ puisque $\forall x \in\left[1,+\infty\left[, ~x \geq 1 \Rightarrow \frac{1}{x} \leq 1\right.\right. \\[0.3cm]$ 3- Les deux fonctions: $h_{1}(x)=\sin (x)$ et ${h}_{2}(x)=\cos (x) $ sont bornées car :
$ \forall x \in \mathbb{R} ,~-1 \leq \sin (x) \leq 1 \quad$ et $\quad-1 \leq \cos (x) \leq 1 $
Interprétation géométrique :
1- Le graphe d’une fonction majorée par $M$ situé au-dessous de la droite $y=M $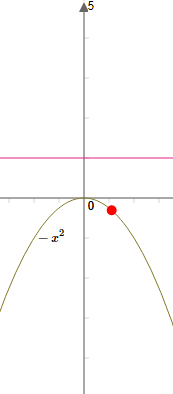 
$\\$La fonction ici c'est $ f(x)=-x^{2}$ est majorée par $1$ car $-x^{2} \leq 0 \leq 1 \\[0.3cm]$ 2- Le graphe d’une fonction minorée par $m$ situé au-dessus de la droite $y=m $ 
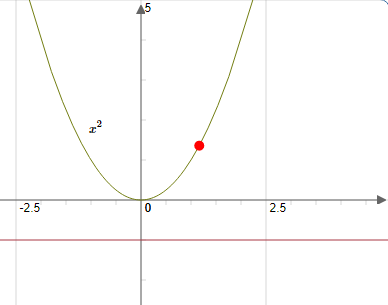$\\$La fonction ici c'est $ f(x)=x^{2}$ est minorée par $-1$ car $x^{2} \geq 0 \geq-1 \\[0.3cm]$ 3- Le graphe d’une fonction bornée situé entre deux droites $ y=M$ et $y=m $ 
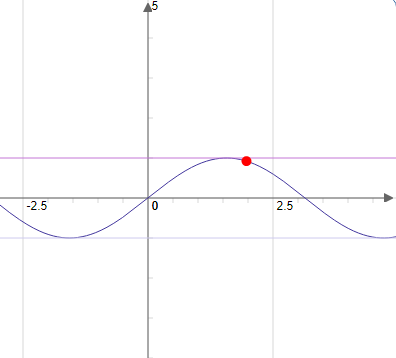$\\$La fonction ici c'est $ f(x)=\sin (x) $
Comparaison de deux fonctions
تعريف
Soit $f$ et $g$ deux fonctions numériques à variable réelle définie, respectivement sur $D$ et $D'$ ; et soit $E$ une partie commune de $D$ et $D'\\[0.2cm]$ On dit que la fonction $f$ est plus petite ou égale à la fonction $g$ , si pour tout élément $x$ de $E$ : $~f(x) \leq g(x) \\[0.2cm]$ On écrit alors : $~f \leq g~$ sur $E~$ ( ou $~g \geq f ~$ sur $E$ )
Remarque
$\bullet$ Si $~\forall x \in E , ~~f(x) < g(x),~$ on dit que la fonction $f$ est strictement inférieure à la fonction $g$ ( ou $f$ est strictement plus petite que $g$ ) $\\[0.2cm]$ $\bullet$ Si $~f \leq g ~$ sur $E$ , alors la courbe représentative de $f$ sur $E$ est située au-dessous de la courbe représentative de $g$ sur $E$.
تعريف
Soit $f$ et $g$ deux fonctions numériques à variable réelle. $\\[0.2cm]$ On dit que les deux fonctions $f$ et $g$ sont égales à : $\\[0.2cm]$ - $f$ et $g$ ont le même ensemble de définition $D\\[0.2cm]$ - et $~\forall x \in D : ~f(x) =g(x) \\[0.2cm]$ On écrit alors : $~f=g$
Les extremums d’une fonction
Extremums absolus
تعريف
Soit $ f $ une fonction numérique de domaine définition $ D_{f}$, soit $ \alpha \in D_{f} $
- On dit que la fonction $ f$ admet un maximum absolu en $ \alpha$ ou le nombre $f(\alpha)$ est un maximum absolu si et seulement si
$\forall x \in D_{f}, \quad f(x) \leq f(\alpha)\\$
On écrit, $ \quad\max _{x \in D_{f}} f(x)=f(\alpha)\\[0.2cm]$
- On dit que la fonction $f$ admet un minimum absolu en $\alpha$ ou le nombre $f(\alpha)$ est un minimum absolu si et seulement si
$\forall x \in D_{f}, \quad f(x) \geq f(\alpha)\\$
On écrit, $\quad \min _{x \in D_{f}} f(x)=f(\alpha)$
Résultats :
- Si $f$ admet un maximum absolu en $\alpha$ alors $f(\alpha)$ est un majorant de $f$ sur $D_{f}\\[0.2cm] $
- Si $f$ admet un minimum absolu en $\alpha $ alors $f(\alpha)$ est un minorant de $f$ sur $D_{f} $
Extremums relatifs
تعريف
Soit $f $ une fonction numérique de domaine définition $D_{f} $
- On dit que la fonction $f $ admet un maximum relatif en $\alpha$ s'il existe un intervalle ouvert $I \subset D_{f} $ contenant $\alpha$ tel que :
$\forall x \in I,~~ f(x) \leq f(\alpha) \\[0.2cm]$
- On dit que la fonction $f$ admet un minimum relatif en $\alpha$ s'il existe un intervalle ouvert $I \subset D_{f}$ contenant $\alpha$ tel que :
$\forall x \in I, ~~f(x) \geq f(\alpha)$
Résultats
Un extrême absolu est relatif mais le contraire ce n’est pas toujours correct.
حيلة
- $M$ est un maximum de la fonction $f \Leftrightarrow $ ($f$ est majorée par $M$ et l'équation $f(x) = M$ admet une solution) $\\[0.2cm]$
- $m$ est un minimum de la fonction $f \Leftrightarrow $ ($f$ est minorée par $m$ et l'équation $f(x) = m$ admet une solution)
تطبيق
Soit $f$ la fonction définie par $ f(x)=\frac{2 x^{2}+7 x+7}{x^{2}+3 x+3} $
- Déterminer $ D_{f} $
- Montrer que $f$ est majorée par $ \frac{7}{3} $ et minorée par$1$
- En déduire que $\frac{1}{3}$ est un maximum et $ 1 $ est un minimum
حيلة
Pour montrer que la fonction $f$ est majorée par $M$ ou minorée par $m$ on effectue la différence entre le nombre et la fonction puis on vérifie le signe du résultat obtenu
Corrigé de l’exercice
1- La fonction est une fraction alors, $D_{f}=\left\{x \in \mathbb{R} / x^{2}+3 x+3 \neq 0\right\}\\[0.2cm]$ Puisque $~\Delta=3^{2}-4 \times 3=-3<0~$ donc $~x^{2}+3 x+3>0~$ (signe de coefficient de $x^{2}$ ) $\\[0.2cm]$ D'où $D_{f}=\mathbb{R}\\[0.3cm]$ 2- L’astuce de cette question c’est d’effectuer à chaque fois la différence entre le nombre et la fonction puis on vérifie le signe du résultat obtenu.
- $f(x)-1=\frac{2 x^{2}+7 x+7}{x^{2}+3 x+3}-1=\frac{x^{2}+4 x+4}{x^{2}+3 x+3}=\frac{(x+2)^{2}}{x^{2}+3 x+3} \geq 0\\[0.2cm]$ car $(x+2)^{2} \geq 0~$ et $~x^{2}+3 x+3>0\\[0.2cm]$ donc $\quad \forall x \in \mathbb{R}, ~~f(x) \geq 1~~$ d'où le résultat $\\[0.2cm]$
- $\frac{7}{3}-f(x)=\frac{7}{3}-\frac{2 x^{2}+7 x+7}{x^{2}+3 x+3}=\frac{x^{2}}{3\left(x^{2}+3 x+3\right)} \geq 0\\[0.2cm]$ car $x^{2} \geq 0$ et $ x^{2}+3 x+3>0\\[0.2cm]$ donc $\quad \forall x \in \mathbb{R}, ~~f(x) \leq \frac{7}{3} ~~$ d'où le résultat.$\\[0.3cm]$
3. $1$ est minimum car l'équation $f(x)=\frac{2 x^{2}+7 x+7}{x^{2}+3 x+3}=1~$ admet une solution dans $\mathbb{R}.\\[0.2cm]$ En effet, $\\$
$\begin{aligned} \frac{2 x^{2}+7 x+7}{x^{2}+3 x+3}=1 & \Leftrightarrow 2 x^{2}+7 x+7=x^{2}+3 x+3 \\ & \Leftrightarrow x^{2}+4 x+4=(x+2)^{2}=0\\ &\Leftrightarrow x=-2 \end{aligned}$ $\\[0.2cm]$ Donc $\quad \forall x \in \mathbb{R}, ~~f(x) \geq f(-2)$ $\\[0.2cm]\frac{7}{3}$ est un maximum puisque $f(0)=\frac{7}{3}~$ donc $~\forall x \in \mathbb{R} \quad f(x) \leq f(0)$
Les variations d’une fonction
تعريف
Soit $ f $ une fonction numérique de domaine de définition $ D_{f}$ et $I \subset D_{f}$ un intervalle.
- $f$ est une fonction croissante sur l'intervalle $I$ cela revient à écrire:
$\forall(x, y) \in I^{2}, \quad x \leq y \Rightarrow f(x) \leq f(y) $
- $f $ est une fonction strictement croissante sur l'intervalle $ I$ cela revient à écrire:
$\forall(x, y) \in I^{2}, \quad x<y \Rightarrow f(x)<f(y) $
ما يجب معرفته
La fonction croissante garde le même ordre des éléments.
Interprétation géométrique :
تطبيق
- $ f(x)=2 x,\quad$ fonction strictement croissante sur $\mathbb{R}$
- $ f(x)=\frac{x^{4}}{2},\quad$ fonction strictement croissante sur $\mathbb{R}^{+} $
- $f(x)=\sqrt{x},\quad$ fonction strictement croissante sur $\mathbb{R}^{+} $
تعريف
Soit $ f $ une fonction numérique de domaine de définition $ D_{f}$ et $ I \subset D_{f}$ un intervalle.
- $ f$ est une fonction décroissante sur l'intervalle $I$ cela revient à écrire:
$\forall(x, y) \in I^{2}, \quad x \leq y \Rightarrow f(x) \geq f(y) $
- $ f$ est une fonction strictement décroissante sur l'intervalle $I$ cela revient à écrire :
$\forall(x, y) \in I^{2}, \quad x<y \Rightarrow f(x)>f(y) $
ما يجب معرفته
La fonction décroissante ne garde pas le même ordre des éléments
Interprétation géométrique :
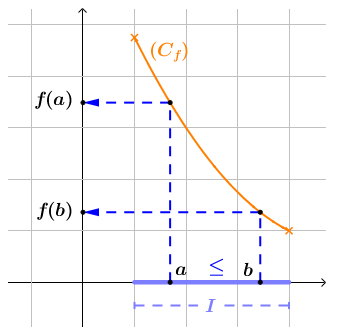
تطبيق
- $ f(x)=-x,~$ fonction strictement décroissante sur $\mathbb{R}$
- $ f(x)=\frac{1}{x},~$ fonction strictement décroissante sur $\mathbb{R}^{*+}$
تعريف
Soit $f$ une fonction numérique de domaine définition $D_{f}$ et $I \subset D_{f} $ un intervalle.
- On dit que $f$ est monotone sur l'intervalle $ I$ si elle est croissante ou décroissante sur $I $.
- On dit que $f$ est strictement monotone sur l'intervalle $I $ si elle est strictement croissante ou strictement décroissante sur $I.$
ما يجب معرفته
Une fonction qui s'écrit sous forme $f(x)=a$ avec $a \in \mathbb{R}$ est dite constante.
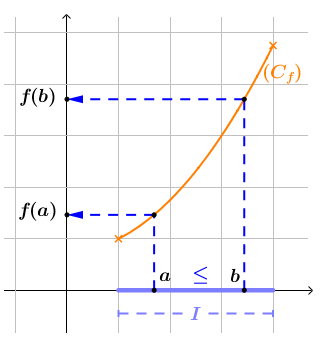
Le taux de variation
تعريف
Soit $f$ une fonction numérique de domaine définition $D_{f}, ~I \subset D_{f}$ un intervalle et $(a, b) \in I^{2}$ tel que $a \neq b .\\[0.2cm]$ Alors, le nombre $T_{(a, b)}=\frac{f(a)-f(b)}{a-b}$ s'appelle le taux d'accroissement ou de variation de la fonction $f$ entre $a$ et $b$.
نظرية
Soit $f$ une fonction numérique de domaine définition $D_{f},~ I \subset D_{f}$ un intervalle.
- $f$ est croissante sur $I~ \Leftrightarrow~\forall(a, b) \in I^{2} ~/ ~a \neq b, \quad T_{(a, b)} \geq 0 \\[0.2cm]$
- $f$ est décroissante sur $I ~ \Leftrightarrow ~ \forall(\alpha, b) \in I^{2} ~/ ~a \neq b,\quad T_{(a, b)} \leq 0$
تطبيق
1- Soit $f$ la fonction définie par : $\quad \forall x \in \mathbb{R}^{*}, ~~f(x)=\frac{1}{x}$
On considère l'intervalle $: I=\mathbb{R}^{*+}$ alors $f$ est décroissante sur $I\\[0.2cm]$ En effet, soit $(a, b) \in I^{2}~$ avec $~a \neq b, \\$
$T_{(a, b)}=\frac{f(a)-f(b)}{a b}=\frac{\frac{1}{a}-\frac{1}{b}}{a-b}=-\frac{1}{a b} \leq 0\\[0.5cm]$ 2- Soit $g$ la fonction définie par $\forall x \in \mathbb{R}^{+}, ~g(x)=\sqrt{x}\\$ On considère l'intervalle $: J=\mathbb{R}^{+}$ alors la fonction est croissante sur $J\\[0.2cm]$ En effet, $(a, b) \in J^{2},~ a \neq b$,
$T_{(a, b)}=\frac{g(a)-g(b)}{a-b}=\frac{\sqrt{a}-\sqrt{b}}{a-b}=\frac{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}{(a-b)(\sqrt{a}+\sqrt{b})}=\frac{1}{\sqrt{a}+\sqrt{b}} \geq 0\\[0.5cm]$ 3- Soit $g$ la fonction définie par $h(x)=4 x^{2}+1\\$ On considère l'intervalle $: K=\mathbb{R}^{+}~$ alors la fonction $g$ est croissante sur $K\\$ En effet, $(a, b) \in K^{2} ,~a \neq b$ $\\[0.2cm] \begin{aligned}T_{(a, b)}=\frac{h(a)-h(b)}{a-b} &=\frac{4 a^{2}+1-4 b^{2}-1}{a-b} \\&=\frac{4(a-b)(a+b)}{(a-b)}=4(a+b) \geq 0\end{aligned}$
La variation et la parité
خاصية
Soit $f$ une fonction numérique paire de domaine définition $D_{f} .\\$ soit $I \subset D_{f} \cap \mathbb{R}^{+}$ un intervalle et $I^{\prime}$ son symétrique par rapport l'origine.
- Si $f$ est croissante sur $I$ alors elle est décroissante sur $I^{\prime} .$
- Si $f$ est décroissante sur $I$ alors elle est croissante sur $I^{\prime} .\\[0.2cm]$
Soit $f$ une fonction numérique impaire de domaine définition $D_{f}.\\$ soit $I \subset D_{f} \cap \mathbb{R}^{+}$ un intervalle et $I^{\prime}$ son symétrique par rapport l'origine.
- Si $f$ est croissante sur $I$ alors elle est croissante sur $I^{\prime} .$
- Si $f$ est décroissante sur $I$ alors elle est décroissante sur $I^{\prime} .$
ما يجب معرفته
Un intervalle $ I^{\prime}$ est symétrique par rapport à l'origine de $I $ revient à tracer le schéma suivant: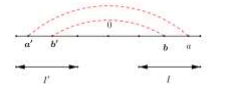 
Par exemple, si $~I=[a, b] ~$ alors $~I^{\prime}=[-b,-a] $
برهان
Nous allons montrer la proposition dans le cas où la fonction $f$ est pair, l'autre cas se fait par le même raisonnement. $\\[0.2cm]$ En effet, on suppose que $f$ une fonction numérique paire de domaine de définition $D_{f} .\\$
soit $I \subset$ $D_{f} \cap \mathbb{R}^{+}$ un intervalle et $I^{\prime}$ son symétrique par rapport l'origine.$\\$
Soit $\left(a^{\prime}, b^{\prime}\right) \in I^{\prime} \times I^{\prime}$ alors
$\\\exists(a, b) \in I \times I ~$ tels que $: ~~a^{\prime}=-a$ et $b^{\prime}=-b\\[0.2cm]$ $T_{f}^{\prime}=\frac{f\left(a^{\prime}\right)-f\left(b^{\prime}\right)}{a^{\prime}-b^{\prime}}=\frac{f(-a)-f(-b)}{b-a}$ $\quad=-\frac{f(a)-f(b)}{a-b}=-T_{f}\\[0.2cm]$
Donc si $f$ est croissante sur $I$ alors $T_{f} \geq 0$ donc
$T_{f}^{\prime} \leq 0 \Rightarrow f~$ est décroissante sur $I^{\prime}$ et vice versa.
Opérations sur les fonctions numériques : somme, produit et quotient de deux fonctions
تعريف
Soit $f$ et $g$ deux fonctions numériques à variable réelle définies, respectivement, sur $D$ et $D'$ tels que : $D \cap D' \neq \empty \\[0.2cm]$ Soit $E$ l'ensemble des points réels communs à $D$ et $D'. \\[0.2cm]$ Soit $F$ l'ensemble des nombres réels $x$ communs à $D$ et $D'$, tels que $~g(x) \neq 0 \\[0.2cm]$ Soit $\lambda$ un nombre réel. $\\[0.2cm]$ 1) La fonction qui à tout élément $x$ de $E$ associe le nombre $f(x)+g(x)~$ est appelée somme des deux fonctions $f$ et $g$ et est notée : $~f+g \\[0.2cm]$ 2) La fonction qui à tout élément $x$ de $D$ associe le nombre $\lambda f(x)$ est appelée produit de $f$f par $\lambda$ et est notée : $~\lambda f \\[0.2cm]$ 3) La fonction qui à tout élément $x$ de $F$ associe le nombre $f(x)\cdot g(x)~$ est appelée produit des deux fonctions $f$ et $g$ et est notée : $~f \cdot g ~$ ou $~fg\\[0.2cm]$ 4) La fonction qui à tout élément $x$ de $F$ associe le nombre $\frac{f(x)}{g(x)}~$ est appelée quotient de la fonction $f$ par la fonction $g$ et est notée : $~\frac{f}{g} \\[0.2cm]$
Remarque
Soient $f$ et $g$ deux fonctions numériques à variable réelle : $\\[0.2cm]$ On pose : $\\[0.2cm]$ $-g= (-1) g \quad ; \quad f-g=f+(-g) \quad ; \quad f^2 =f \cdot f \quad ; \quad f^3=f \cdot f^2 ; \\[0.2cm] \forall n \in \mathbb{N} \backslash\{0 , 1\}, \quad f^n=f \cdot f^{n-1}$
Composée de deux fonctions
تعريف
Soit $f$ la fonction définie sur l'intervalle $I$ et $g$ la fonction définie sur l'intervalle $J\\$ tel que : $f(I) \subset J,$ autrement dit $(\forall x \in I, ~~f(x) \in J)\\$ La composée de $f$ et $g$ est la fonction notée: $g \circ f$ définie sur $I$ par:
$\forall x \in I, \quad g\circ f(x)=g(f(x))\\[0.2cm]$
Le schéma suivant illustre bien les trois fonctions $f, g$ et $g\circ f$ :
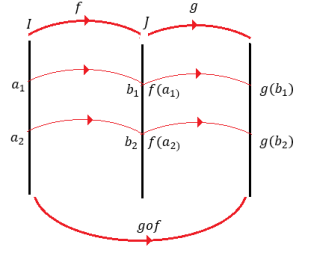
ما يجب معرفته
Le domaine de définition d’une fonction composée est :
$\\[0.2cm]D_{g \circ f}=\left\{x \in \mathbb{R} / ~x \in D_{f} ~~\text { et }~~ f(x) \in D_{g}\right\}$
خاصية
Soient $f$ et $g$ deux fonctions dont les ensembles des définitions respectifs $D_{f}$ et $D_{g}$
soient $I$ un intervalle de $D_{f}$ et $J$ un intervalle de $D_{g}$ tels que $f(I)=J$
- Si $f$ est croissante sur $I$ et $g$ est croissante sur $J=f(I) $ alors $g \circ f$ est croissante sur $I$. $\\[0.2cm]$
- Si $f$ est décroissante sur $I$ et $g$ est décroissante sur $J=f(I)$ alors $g\circ f$ est croissante sur $I$. $\\[0.2cm]$
- Si $f$ est croissante sur $I$ et $g$ est décroissante sur $J=f(I)$ alors $g\circ f$ est décroissante sur $I$. $\\[0.2cm]$
- Si $f$ est décroissante sur $I$ et $g$ est croissante sur $J=f(I)$ alors $g\circ f$ est décroissante sur $I$.
تطبيق
Soit les fonctions $ g(x)=x^{2}+5 x-1$ et $f(x)=3 x+2 $
- Déterminer $ D_{f}, D_{g}$ et $D_{f \circ g }$ et $D_{g\circ f } $
- Calculer $f\circ g$ et $g\circ f $
- Soit $h(x)=\sqrt{x^{2}+1}$ , alors déterminer la monotonie de $h$ sur $\mathbb{R}^{+} $
Corrigé
1- Les fonctions $f$ et $g$ sont polynomiales alors $D_{f}=\mathbb{R}~$ et $~D_{g}=\mathbb{R}\\[0.2cm]$ En plus, $f(\mathbb{R})=\mathbb{R}~$ et $~g(\mathbb{R})=\mathbb{R}$ donc on a le droit de parler de $f\circ g$ et $g\circ f\\[0.2cm]$ D'après la remarque ci-dessus, $ D_{f\circ g }=\mathbb{R}=D_{g\circ f } \\[0.5cm]$ 2- Soit $ x \in \mathbb{R},~$ alors
$f\circ g(x)=f(g(x))=f\left(x^{2}+5 x-1\right)=3 x^{2}+15 x-1 \\$
Soit $x \in \mathbb{R}, $ alors :
$\begin{aligned} g\circ f(x)&=g(f(x))\\ &=g(3 x+2) \\ &=(3 x+2)^{2}+5(3 x+2)-1\\ &=9 x^{2}+27x+13\end{aligned}$
حيلة
Nous déterminons la monotonie d’une fonction non usuelle en cherchant à l’écrire comme une composée de deux fonctions dont la monotonie est connue.
$x \leq y \Rightarrow x^{2} \leq y^{2}$ $\Rightarrow x^{2}+1 \leq y^{2}+1 \Rightarrow h_{1}(x) \leq h_{2}(y)$
et $~h_{2}\left(\mathbb{R}^{+}\right)=\left[1,+\infty\left[\right.\right.\\[0.2cm]$ en effet : soit $x \in \mathbb{R}^{+} \Rightarrow x^{2}+1 \geq 1$ $\Rightarrow h_{2}(x) \in[1,+\infty[\\[.2cm]$ Inversement, soit $x \in[1,+\infty[$ on pose $y=\sqrt{x-1}\\$
Donc $x=y^{2}+1$ avec $y \in \mathbb{R}^{+}~\Rightarrow x \in h_{2}\left(\mathbb{R}^{+}\right) \\$
Par la suite, $h_{1}$ est croissante sur $[1,+\infty[\\$
Donc, $h$ est croissante sur $\mathbb{R}^{+}$
Les fonctions périodiques
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo
- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon
Signaler une erreur